Strange PE of Elliptical Orbits

-A curious relationship between potential energy and kinetic energy-

I came up this question during my high school lesson on orbits. And, you know, it's hard to understand a concept completely relying on a naive child's brain. At times this explanation might seem - I wouldn't say misleading - forced by convention, but after more insights it actually works out best.

The conundrum

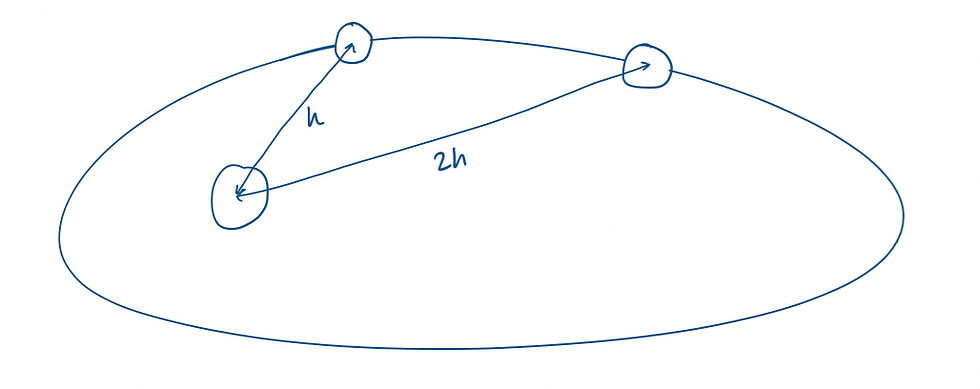
Let's check out a diagram first. A planet is peacefully orbiting its star in a nice, elliptical orbit. At one time, it has a distance h to the star, after a certain period of time, it has distance 2h.

We also know (hopefully) from our high school lesson the formulae for gravitational potential energy, kinetic energy and the force of gravitational attraction. From the law of conservation of energy, we know the sum of kinetic energy and gravitational potential energy (collectively known as mechanical energy) is conserved. Like this.

(the small g is the gravitational field strength at a certain point, we can multiply that by an object's mass to get its weight)

So logically, as distance increases with time, the GPE should increase because:

1. The planet is further away from the star

2. Kinetic energy decrease, energy conservation

Right?

Nope. Not really. If we do the calculation of the gravitational potential energy mgh at a distance of 2h:

It's half of what we had. So why does GPE decrease while the planet decrease, especially, when the kinetic energy also decrease?

Hmm.... I wonder why? Worthy of musings.

---

My answer for now:

There's one thing wrong here. Gravitational potential energy is actually negative. Why? Because it's a convention (elegant English noises). Well who knew?

But actually, if you think about it intuitively, it does make sense. The gravitational force is a force with an infinite range, thus you technically gets attracted to a thing millions of light years away from you, but just a little bit. Complete freedom is 0 GPE, no problem, since there is no "potential" for you to fall towards anything and releasing that "potential". Right? Right.

I'll put a derivation here... but it's not that important.

But with all this negative stuff, does GPE still increase as we go farther away from the object? Well yes, despite being all negative, GPE gets less and less negative farther and farther away -> i.e. an increase. On Earth, we normally assume GPE = 0 at the Earth's surface, but it works the same.

So the key takeaway is that GPE always ≤ 0. Back to our initial conundrum, with the minus sign, GPE actually increases as h/r increases because all GPE is either negative or zero. When distance increse, GPE becomes less negative so it's indeed increasing!